In my previous post I showed how you can calculate matrix elements for representatives of SU(3) group elements in the $(p,0)$ irreps. That post had been sitting around in a partially finished state for a long time, so I pushed it out without adding any visualizations, which is a shame because the visualizations are my favorite part! Visualizing complex matrices is tricky, though. In the past I’ve visualized the real and imaginary parts of the matrix separately using the representation for real matrices used in my original SU(3) post (using a diverging colormap for positive/negative). I’ve also tried a 2-d colormap like I used in my tetrahedral irrep post (with hue encoding the complex phase and brightness encoding the amplitude), but the matrix entries are discontinuous, which means you can’t get away with quite as much dynamic range (in the tetrahedral plots, the largest values were almost white, but you could infer the hue from neighboring patches). This reduction in dynamic range made it very hard to see much detail in these kinds of plots.

What I ended up settling on was a variation on a Hinton diagram. Each matrix element is represented by a square. The area of the square is proportional to the absolute value of the matrix element, just like in a Hinton diagram. However, instead of just using white and black for positive and negative entries, I color the squares using a cyclic colormap to indicate their phases. My favorite option for this is the cyclic_isoluminant colormap provided by colorcet. To illustrate this in action, here is the representative for the SU(3) discrete-Fourier-transform matrix in the $(3,0)$ irrep:

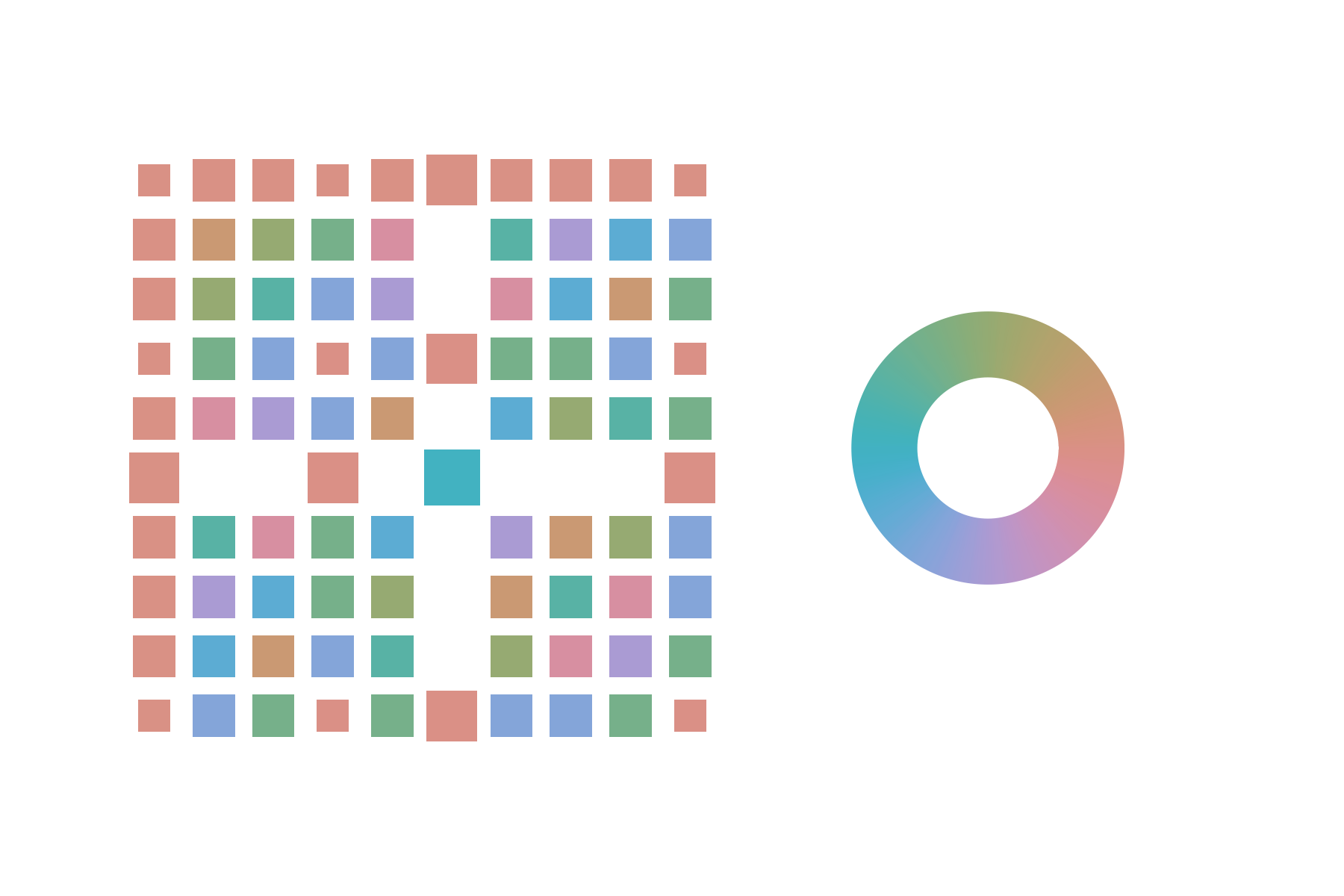
I think it looks quite attractive, and is certainly a lot easier to pull information out of that a printout of the numpy array. The proportionality of the area to the absolute value gives you very nice dynamic range (since there’s a quadratic visual effect with respect to the linear dimensions). The annulus to the right serves as a colorbar, reminding us which colors correspond to which phases on the unit circle in the complex plane. I put the code used to generate this kind of plot in the same repository for the SU(3) calculations, in the function complex_hinton_plot, so have fun playing around with that!