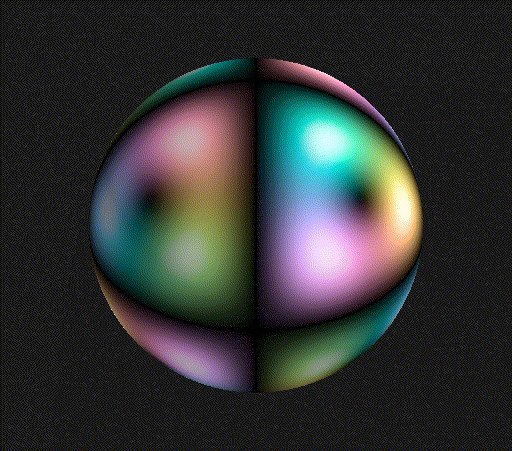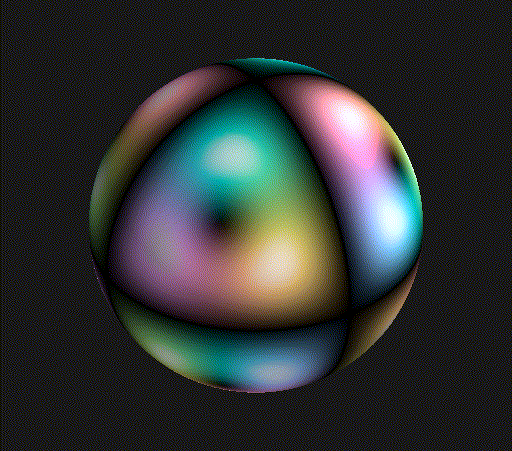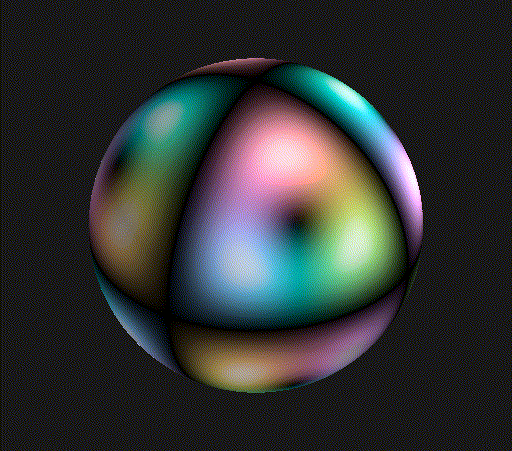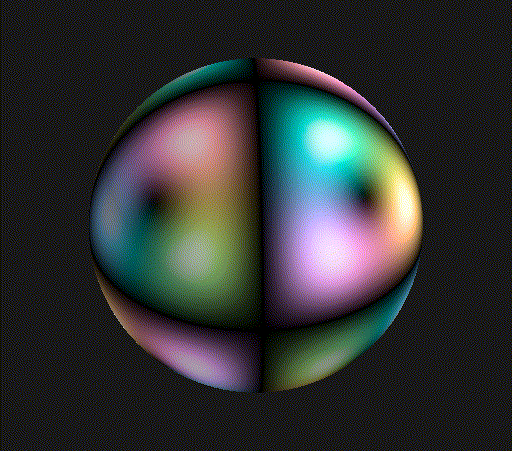
Lately I’ve been thinking about representations of discrete subgroups of $\mathrm{SU}(2)$ for my recently posted preprint on error-correcting codes for large single spins (which you can scite on SciRate if that’s the kind of thing you’re into!). I’ll have some more to share about that project soon, but right now I just wanted to quickly share a bonus discovery I made that relates to a problem John Baez and Greg Egan have written about.

They were looking for electron orbital wavefunctions for the hydrogen atom that had dodecahedral symmetry, which boiled down to finding trivial irreducible representations of the group of rotational symmetries of the icosahedron/dodecahedron. These one-dimensional representations correspond to wavefunctions that remain unchanged when any of the icosahedron’s symmetries are applied. If you haven’t read either of the posts I linked to above, I recommend you take some time to see how they identify all the symmetric wavefunctions in subspaces of varying angular momentum, and enjoy the stunning renditions of these wavefunctions.

Naturally there’s nothing stopping one from thinking about orbital wavefunctions with different symmetries, and John and Greg both talk about octahedral and tetrahedral symmetry as well. Something interesting happens with these shapes, though, that didn’t happen with the dodecahedron: there are wavefunctions that are changed by application of symmetry operators, but this change is only multiplication by a phase. Multiplication by a global phase doesn’t change the state of a quantum system, though, so these wavefunctions are also invariant under octahedral and tetrahedral rotations!

Reading the Postscript to John’s post, it appears that these nontrivial one-dimensional irreps were discussed in the comments to Greg’s Google+ post on the topic, but since Google+ is no more I can only see a limited number of comments on archived versions via the wayback machine, so I can’t be sure how much they delved into it. I thought it would be fun, then, to visualize some of these additional symmetric wavefunctions. The tetrahedral irreps are a little more fun, since they genuinely require complex numbers for there description, so I’ll just give a taste of them for now.

The nontrivial one-dimensional tetrahedral irreps come in pairs which are kind of left- and right-handed versions of one-another, so I’ll just focus on one version. The dimensions subspaces with these symmetries are given in the table below for the smallest values of orbital angular momentum $\ell$:

$\ell=0$: dimension 0

$\ell=1$: dimension 0

$\ell=2$: dimension 1

$\ell=3$: dimension 0

$\ell=4$: dimension 1

$\ell=5$: dimension 1

This pattern repeats with period 6, the dimension growing by 1 each time. The Supplemental Material of my recent preprint discusses more details about how I calculated these dimensions, and how to explicitly represent these subspaces. Let’s take a look at what the orbital wavefunction looks like for $\ell=2$ then, the smallest dimensional example! I restrict myself just to the angular parts of the wavefuntion in these plots, which corresponds to the surface of the sphere, with the magnitude of the complex amplitude represented by brightness and the phase of the complex amplitude represented by hue.

Pretty cool! Looks like a cube, where each pair of opposite faces have a different color. The black corners correspond to the axes of threefold rotational symmetry that run through the vertices and centers of faces of the tetrahedron defining the symmetries. You can clearly see that the coloring of the cube changes if you perform one of these rotations by a third of a turn, but the same recoloring is just a rotation in hue caused by multiplying the entire wavefunction by a complex phase.

Let’s move on to $\ell=4$.

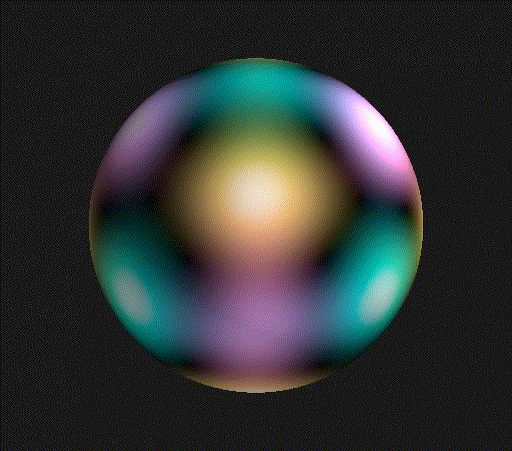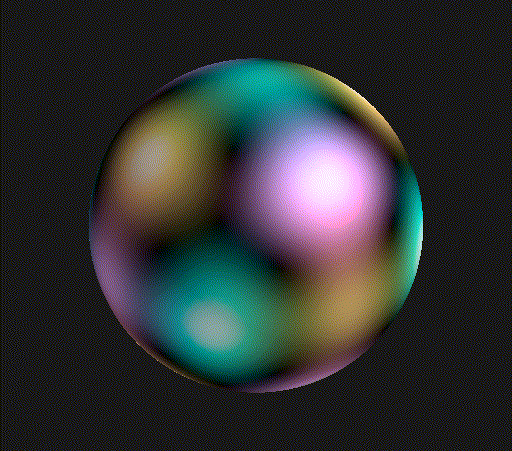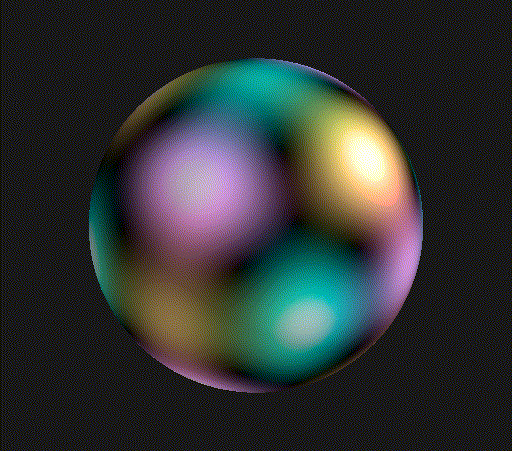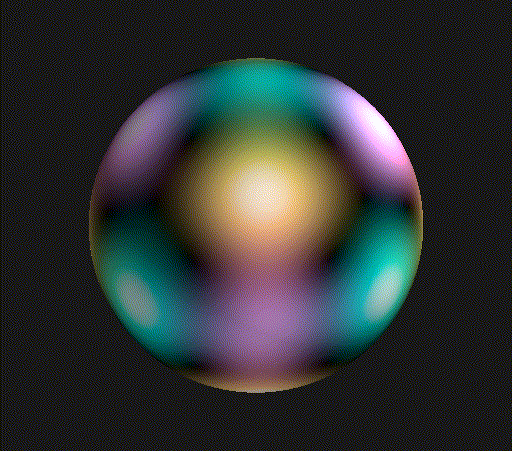
Again, you see points of threefold rotational symmetry, just with a bit finer structure. The picture at the top of the post is the wavefunction for $\ell=5$, which also has some planes along which the wavefunction vanishes that are evocative of an octahedron.

That’s all for now, but next I’ll dive into some visualizations of the two-dimensional irreps of $\mathrm{SU}(2)$ that I used to build error-correcting codes for large spins.